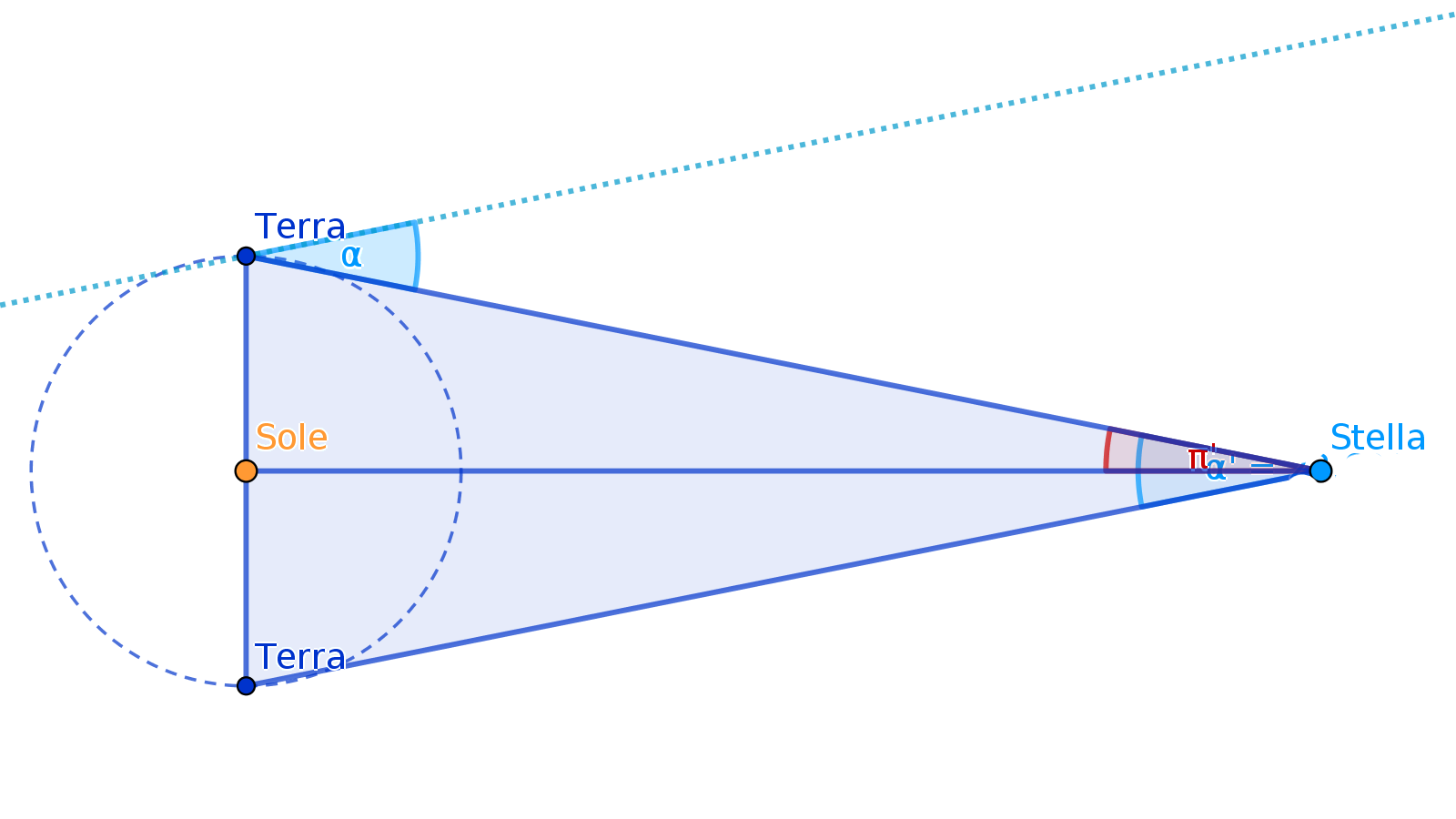
|
Se la Terra gira intorno al Sole la stella lontana dovrebbe essere vista in direzione diversa a sei mesi di distanza (mezzo giro dell'orbita) e dovrebbe essere possibile misurare la variazione di direzione (angolo $\alpha$), che è poi il doppio dell'angolo di parallasse (angolo $\pi$). |
Nel II secolo a.C. Archimede obiettò al modello eliocentrico di Aristarco di Samo il fatto che le stelle remote non presentavano effetti di parallasse. In altri termini se la Terra gira intorno al Sole le stelle dovrebbero apparire in direzione leggermente spostata a distanza di sei mesi; e gli astronomi greci non avevano misurato alcun effetto di parallasse delle stelle. Archimede sapeva bene che le stelle sono a distanze enormi, molto maggiori della distanza Terra-Sole, ma non immaginava che fossero talmente enormi da rendere praticamente impercettibile l'effetto di parallasse. O quanto meno non aveva strumenti abbastanza precisi per risolvere il dubbio.
Solo nel XIX secolo furono costruiti telescopi sufficientemente potenti e precisi da misurare l'effetto di parallasse delle stelle più vicine, e così questo effetto divenne un metodo per misurare la distanza delle stelle.
Il metodo sfrutta il fatto che la Terra, girando intorno al Sole, nell'arco di sei mesi viene a trovarsi a una distanza di circa 300 milioni di km (2 Unità astronomiche) dalla posizione di partenza. Questa distanza fornisce una base sufficiente per risolvere il triangolo rettangolo TSA alla condizione di misurare con sufficiente precisione l'angolo $\pi$, noto come angolo di parallasse.
In pratica per misurare $\pi$ si prendono a distanza di sei mesi, con un telescopio, due lastre fotografiche dello stesso campo stellare; le due lastre vengono sovrapposte a registro: le stelle più lontane che hanno parallasse nulla si sovrappongono esattamente; quelle più vicine mostrano un leggero spostamento. Per correggere il risultato dall'eventuale moto proprio della stella è bene ripetere la misura dopo altri sei mesi e mediare il risultato.
Misurando questo spostamento si misura di fatto l'angolo $\alpha$ che, come risulta evidente dal disegno a lato, è uguale all'angolo $\alpha'$ sotto il quale l'orbita terrestra viene vista dalla stella, essendo alterni interni tra rette parallele. E $\alpha'$ è il doppio dell'angolo di parallasse.
A questo punto dalla definizione trigonometrica di tangente si ricava la formula risolutiva a lato, dove ST è la distanza Terra-Sole. $$ SA = \frac{ST}{\tan{\pi}} = ST \times \cot{\pi} $$
Il problema con questo metodo è che gli angoli di parallasse delle stelle sono estremamente piccoli; la stella più vicina la Proxima Centauri ha un angolo di parallasse di 0.75" circa un quattromillesimo di un grado.
| $$ SA = \frac{ST}{\tan(\pi)} = \frac{1.5 10^{11} m}{\tan(0.00'00''29)} = 1.067 \times 10^{17} m$$ |
| $$ SA = \frac{1.067 \times 10^{17}}{9.467 \times 10^{15} A.L.} = 11.3 Anni Luce $$ |
La prima misura di una parallasse stellare fu compiuta nel 1838 dal grande matematico e astronomo tedesco Friedrich W. Bessell che misurò la parallasse di una piccola stella del Cigno (la 61 Cycni) trovando un valore di 0.29", che equivale a una distanza di circa 11 anni luce, come risulta dal calcolo riportato nella tabella a lato (ricordando che un anno luce equivale a $9.467 \times 10^{15} m$)
Il metodo della parallasse fornisce stime accettabili delle distanze stellari solo per le stelle più vicine al Sole, grosso modo fino a qualche centinaio di anni luce. Per le stelle più lontane esistono altri metodi meno precisi che sono comunque sempre basati sul confronto con la distanza delle stelle vicine, quelle delle quali è nota la parallasse. Molto conosciuto ma non unico è quello delle cefeidi.